Dresser un tableau de variation

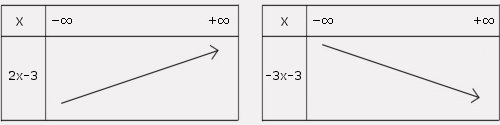
I. Idée générale Le tableau de variation permet d'avoir un aperçu de la représentation graphique d'une fonction. Si, sur un intervalle donné, le tableau de variation donne la fonction décroissante puis croissante, alors on sait que le tracé de la courbe représentative descendra puis montera sur ce même intervalle. II. Fonction affine Une fonction affine est de la forme   y = ax + b a est le coefficient directeur de la fonction. On sait que si a > 0 alors la fonction est croissante, si a < 0 alors la fonction est décroissante. On peut donc rapidement dresser le tableau de variation, qui confirme la représentation graphique de la fonction affine (une droite). III. 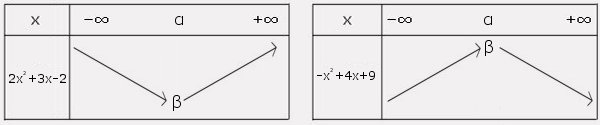Fonction du second degré Une fonction polynome de degré 2 est de la forme   y = ax2 + bx + c a est le coefficient directeur de la fonction. On sait que si a > 0 alors la fonction est décroissante puis croissante, si a < 0 alors la fonction est croissante puis décroissante. 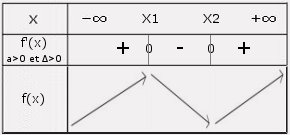On cherche à savoir quand la fonction changera de sens, c'est-à-dire le sommet S (α;β)          α = -b/2a         β = f(α) On dessine maintenant le tableau de variation IV. Fonction cube Une fonction cube comporte un x3                 ex: f(x) = 3x3 - 2x2 - 5x - 8 . On commence par dériver la fonction f(x) et on obtient un polynome du second degré.                 f'(x) = 9x2 - 4x - 5 . On calcule le discriminant (Δ = b2 - 4ac)                       Si Δ < 0 il n'y a pas de racine, donc la courbe représentative de la dérivée ne coupe pas l'axe des abscisses.                       Si Δ = 0 il y a une racine (x = -b/2a), donc la courbe représentative de la dérivée a son sommet sur l'axe des abscisses.                       Si Δ > 0 il y a deux racines ( X1 = -b-√Δ)/2a   et   X2 = -b+√Δ)/2a ), donc la courbe représentative de la dérivée coupe l'axe des abscisses en deux points d'abscisse X1 et X2. . On construit le tableau de signes de la fonction dérivée . On dresse enfin le tableau de variation de la fonction f. Quand la fonction dérivée est positive, la fonction d'origine est croissante, quand la fonction dérivée est négative, la fonction d'origine est décroissante. 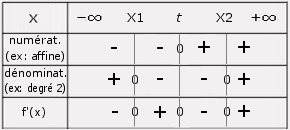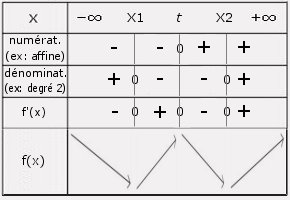V. Fonction homographique Une fonction homographique est de la forme u(x) / v(x)                 ex: f(x) = (x2 - 2) / (2x2 - x + 3) . On commence par dériver la fonction f(x) par la formule de dérivation u / v → (u'v - uv') / v2 . On obtient alors le quotient de deux fonctions intermédiaires. On cherche le signe de chacune d'elles avec les méthodes ci-dessus et on construit le tableau de signes de la dérivée. . On trace maintenant le tableau de variation de la fonction f selon la même méthode que celle de la fonction cube.  programme officiel     |     contactez un professeur     |     cours particuliers     |      haut de la page