Correction des exercices de Calcul littéral

Exercice I A = 2(4x + 8) + 4(2x − 5) A = 8x + 16 + 8x – 20 A = 16x – 4 B = 5x(2x − 7) − x(2x − 3) B = 10x2 − 35x − 2x2 + 3x B = 10x2 − 32x C = (2x + 3)(5x − 8) − (2x − 4)(5x − 1) C = 10x2 – 16x + 15x – 24 – 10x2 +2x + 20x – 4 C = 21x − 28 D = (5/4 + x/3)(x/3 − 5/4) D = 5x/12 - 25/16 + x2/9 - 5x/12 D = x2/9 – 25/16 Exercice II A = (x + 6)(2x − 1) + (x + 6)(3x + 2) A = (x + 6)(2x − 1 + 3x + 2) A = (x + 6)(5x + 1) B = (4x + 2)(7x − 1) − (4x + 2)(5x − 4) B = (4x + 2)(7x − 1 − 5x + 4) B = (4x + 2)(2x + 3) C = (6x – 9)2 + (6x – 9)(y – 1) + 6x – 9 C = (6x − 9)(2x − 5 + y − 1 + 1) C = (6x − 9)(2x + y − 5) Exercice III A. −2(6x − 1) = 8x − (−3 + x) −12x + 2 = 8x + 3 − x −12x −8x + x = 3 − 2 −19x = 1 x = -1/19 B. 5(9x − 3)(−5x − 13) = 0 soit 9x – 3 = 0 soit –5x – 13 = 0 9x = 3 ou -5x = 13 L'ensemble des solutions de l'équation sont 1/3 et −13/5 Exercice IV un nombre entier x x au carré     =>     x2 Doubler le résultat    =>     2x2 Le produit de x par l'entier qui le suit     =>     x(x+1) Soustraire au résultat précédent ce produit     =>     2x2 - x(x+1) Après développement     =>     2x2 - x2 - x = x2 - x Après factorisation     => x(x – 1) => Ce programme revient à multiplier un nombre par celui qui le précède. 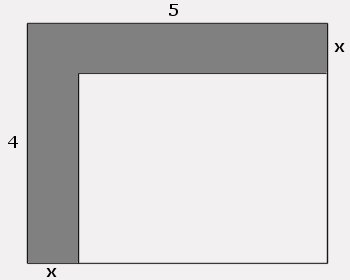Exercice V     Les quatre expressions littérales suivantes permettent de calculer l'aire de la figure foncée.      A = 5x + 4x - x2      B = 4x + x(5-x)      C = 5x4 - (5-x)(4-x)      D = 5x + x(4-x) Montrer que A = B = C = D A = 5x + 4x - x2 = 9x - x2 B = 4x + x(5-x) = 4x + 5x - x2 = 9x - x2 C = 5x4 - (5-x)(4-x) = 20 - 20 + 5x + 4x - x2 = 9x - x2 D = 5x + x(4-x) = 5x + 4x - x2 = 9x - x2 Exercice VI Un parc d'attractions peut accueillir 800 visiteurs, dont x enfants. Les places "adulte" coûtent 15€ et les places "enfant" 10€. 1:. A quoi correspondent les expressions:      A = 800 – x 800-x est le nombre de visiteurs adultes.      B = 10x 10x est la recette générée par les entrées "enfant".      C = 15x 15x ne correspond à rien pour cet énoncé (15 est le prix d'un billet "adulte" et x le nombre d'enfants).      D = 15(800 – x) 15(800 – x) est la recette générée par les entrées "adulte". 2:. Exprimer en fonction de x la recette totale (en euros) lorque tous les billets sont vendus. 10x + 15(800 – x) 3:. Calculer la recette du parc d'attractions si x = 200. 10 x 200 + 15(800-200) = 2000 + 15 x 600 = 2000 + 9000 = 11 000€ 4:. Quel est le nombre de places "enfant" vendues si le parc affiche "complet" avec une recette de 15 000 € ? 10x + 15(800 – x) = 15 000 10x + 12 000 - 15x = 15 000 -5x = 3000 x = -600 Donc avec cette valeur de x (négative!) on en déduit qu'il est impossible que le parc génère une recette de 15 000€. Cela se vérifie en multipliant le nombre maximum d'entrées (800) par le prix le plus élevé (15€), ce qui donne 12 000€! Exercice VII Un mentaliste demande à un spectateur de suivre ses instructions:     . Choisissez un nombre;     . Multipliez-le par -11;     . Ajoutez 8;     . Multipliez le résultat par -9;     . Ajoutez le nombre choisi au départ;     . Ajoutez -28;     . Donnez votre résultat . Le spectateur a trouvé 400. Immédiatement, le mentaliste devine qu'il avait choisi 5 au départ. Quel est son "truc"? Le programme de calcul du mentaliste vaut pour x un nombre choisi au hasard: -9(-11x + 8) + x + (-28) = 99x - 72 + x - 28 = 100x - 100 Ainsi bien plus rapide pour le calcul mental permettant d'obtenir 400! fermer la page   programme officiel     |     contactez un professeur     |     cours particuliers     |      haut de la page