|
Correction des exercices sur les bissectrices
Exercice I
1. Tracer la bissectrice de chacun des angles d'un triangle ABC tel que AB = 7cm, BC = 3cm, AC = 5cm.
2. Que peut-on constater?
Les bissectrices sont concourantes.
Exercice II
1. Tracer un cercle de centre O puis un diamètre [DI].
2. Tracer la mediatrice de [DI]qui coupe le cercle en M et E.
3. Tracer la bissectrice de 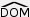 . Une fois prolongée elle coupe le cercle en deux points. . Une fois prolongée elle coupe le cercle en deux points.
4. Tracer la bissectrice de 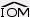 . La prolonger pour qu'elle coupe le cercle en deux points. . La prolonger pour qu'elle coupe le cercle en deux points.
5. Nommer et identifier la figure obtenue (nom de polygone).
DT'ERIR'MT est un octogone régulier.
Exercice III
La droite (NH) est perpendiculaire à la droite (PZ). Les deux droites se coupent en G.
Prouver que (NH) est la bissectrice de 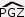 . .
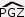 est un angle plat, donc de 180°. (NH) étant perpendiculaire à (PZ), les deux droites forment un angle droit, donc est un angle plat, donc de 180°. (NH) étant perpendiculaire à (PZ), les deux droites forment un angle droit, donc 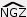 mesure 90°, soit la moitié de 180°. mesure 90°, soit la moitié de 180°.
Or la bissectrice d'un angle coupe cet angle en deux angles égaux, donc (NH) est la bissectrice de 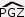 . .
Exercice IV
Lors du lancer d'un poids, le lanceur le projette selon la trajectoire suivante.
Pour améliorer son résultat, l'entraineur lui propose de diviser par deux l'angle de lancer.
1. Sur la figure donnée, représenter le nouvel angle.
2. Calculer cet angle et justifier la réponse.
On mesure l'angle du premier lancer: 66°.
Comme la bissectrice coupe un angle en deux angles égaux, le nouvel angle est de 66 : 2 = 33°.
|
|