|
Correction des exercices sur les médianes, médiatrices et hauteurs
Exercice I
Une planche de bois triangulaire, de dimensions 50cm x 40cm x 80cm doit être placée en équilibre.
1. Convertir ces mesures en décimètres.
40cm = 4 dm
50cm = 5 dm
80cm = 8 dm
2. En prenant pour échelle 1dm → 1cm, tracer le triangle et définir son centre de gravité, c'est-à-dire son point d'équilibre.
|
|
Le centre de gravité d'un triangle
est le point d'intersection des médianes. |
Exercice II
Tracer le cercle circonscrit au triangle TRI tel que TR = 9 cm, 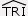 = 100° et RI = 7 cm. = 100° et RI = 7 cm.
|
|
Le centre circonscrit d'un triangle
a pour centre le point d'intersection des médiatrices. |
Exercice III
Dans le triangle ABC, les médianes issues de B et C se coupent en I. Justifier que la droite (AI) est la médiane issue de A.
|
|
Les trois médianes d’un triangle sont concourantes.
Dans le triangle ABC,
I est le point d’intersection de deux médianes,
donc le point de concours des trois médianes.
La droite passant par le sommet A et par I est donc la médiane issue de A.
|
Exercice IV
1. Tracer un triangle ABC avec BC = 8 cm ; AB = 6 cm ; AC = 4 cm.
2. Tracer la médiatrice (m) de [BC].
3. Tracer la hauteur (h) issue de A.
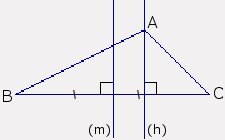
4. Démontrer que les droites (h) et (m) sont parallèles.
(h) est la hauteur issue de A, donc perpendiculaire à (BC).
(m) est la médiatrice de [BC], donc perpendiculaire à (BC).
Or si deux droites sont perpendiculaires à une même troisième droite alors elles sont parallèles entre elles.
Donc (h) est parallèle à (m).
Exercice V
1. Construire un triangle ABC isocèle en A avec BC = 7 cm et AB = 9 cm.
2. Tracer la médiatrice (m) de [BC].
3. Tracer la hauteur (h) issue de A.
4. Tracer la médiane (n) issue de A.
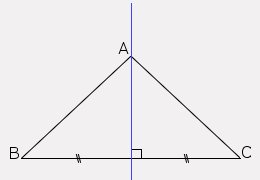
5. Que peut-on dire des droites (m), (n) et (h)?
Les droites (m), (n) et (h) sont superposées.
Exercice VI
1. Construire le triangle GEL avec GL = 7 cm ; GE = 8 cm ; EL = 10 cm.
2. Tracer en rouge les médiatrices de [GL] et [EL].
3. Tracer en bleu les médianes issues de G et E.
4. Tracer en vert les hauteurs issues de G et E.
5. Tracer le cercle circonscrit du triangle.
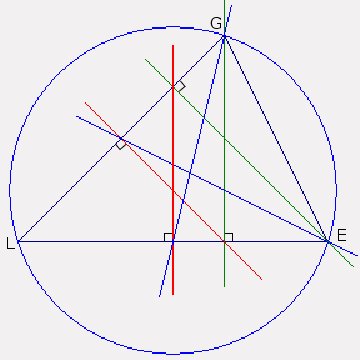
|
|