|
Exercices sur la symétrie centrale
Exercice I
Déterminer le centre de symétrie de chaque figure s'il existe.
1:.
|
2:.
|
3:.
|
4:.
|
5:.
|
6:.
|
7:.
|
8:.
|
9:.
|
Exercice II
1:. Reproduire la figure.
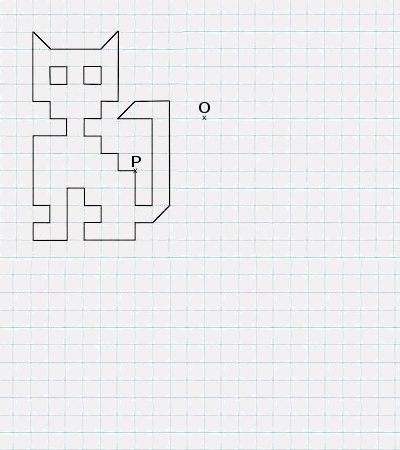
2:. Tracer le symétrique par rapport au point O.
3:. Tracer le symétrique par rapport au point P.
Exercice III
Compléter les phrases.
1:. Le point M' est le symétrique du point M par rapport à O, c'est-à-dire que
est le milieu du segment
[]
.
2:. Le point T est le milieu du segment [IR] c'est-à-dire que
et
sont symétriques par
rapport à
.
3:. Le point
est l'image du point G dans la symétrie de centre C, c'est-à-dire que
est le milieu du segment [G
]
.
4:. Le segment [U
] a pour milieu le point
, c'est-à-dire que le point F est le symétrique du point
par rapport à B.
Exercice IV
On considère le triangle TRI tel que TR = 4,5cm, TI = 6cm et RI = 4cm.
1:. Construire ce triangle.
2:. Tracer les symétriques T’ et I’ des points T et I par rapport à R.
3:. Construire le triangle T’RI’.
4:. Que peut-on dire des segments [TI] et [T'I']? Justifier.
5:. Quel angle a la même mesure que l’angle 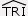 ? Justifier. ? Justifier.
|