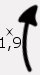Proportionnalité, échelle et pourcentage

I. Grandeurs proportionnelles Deux grandeurs sont proportionnelles si on peut multiplier les valeurs de chacune des deux par un même nombre appelé coefficient de proportionnalité. La vente au poids ou au litre par exemple applique la proportionnalité. On nous donne le prix du kilogramme ou du litre, et ainsi on peut connaître le prix en fonction de la quantité achetée.                ex: Les tomates sont vendues 1,90 € le kilo.                      Donc 1 kg coûte 1,90 €.                      Grâce à la proportionnalité, je peux conaître le prix de 12 tomates,                      qui pèsent 1,5 kg.                      Pour passer de 1kg à 1,5kg:                      1kg x 1,5 = 1,5kg                      On multiplie alors:                      1,90€ x 1,5 = 2,85€                      Le prix de 1,5kg de tomates est donc de 2,85€.          On dit alors alors que le prix est proportionnel à la quantité (en kg) achetée. II. Tableau de proportionnalité 1:. Ce tableau comporte deux lignes correspondant aux deux grandeurs proportionnelles. On peut alors trouver les valeurs de l'une ou l'autre ligne en appliquant un coefficient multiplicateur.  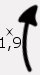Prix des tomates (en €) 1,90 2,85  Poids des tomates (en kg) 1 1,5 Ainsi, à chaque fois qu'on a le chiffre de la première ligne, on divise par le coefficient pour trouver la deuxième ligne, et inversement quand on a le chiffre de la deuxième ligne, on multiplie par le coefficient pour trouver la première ligne.  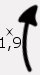Prix des tomates (en €) 1,90 2,85 4,50 ?  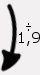Poids des tomates (en kg) 1 1,5 ? 8                      4,50 : 1,9 = 2,37                      Pour 4,50€, on achète 2,37kg de tomates.                      8 x 1.9 = 15,2                      8kg de tomates coûtent 15,2€. 2:. On peut aussi passer d'une case à une autre horizontalement, d'une colonne à une autre, toujours avec un coefficient multiplicateur.                 Prix des tomates (en €) 1,90 3,80  Poids des tomates (en kg) 1 2                Ainsi dans un tableau comme celui-ci:  Prix des tomates (en €) 1,90 3,80 ? 19,00  Poids des tomates (en kg) 1 2 5 ? On remarque qu'il y a 5 fois 1kg de tomates, donc le prix sera 5 fois celui du kilogramme.                      5 x 1,90 = 9,50€ On remarque aussi que dans la quatrième colonne le prix des tomates est 10 fois plus élevé que le prix au kg (1,9 x 10 = 19). La quantité sera alors 10 fois supérieure au kilo initial.                      1 x 10 = 10kg III. Echelle Une échelle sert à reproduire un objet ou une carte par exemple, mais dans des dimensions plus petites. On ne peut en effet pas créer une carte de la France avec les mesures réelles! Mais sur la maquette ou le plan, les distances doivent être proportionnelles aux distances réelles. Une échelle est donc le coefficient de proportionnalité qui permet de passer des mesures du modèle réduit aux mesures réelles, celles-ci étant exprimées dans la même unité.                ex: Si on lit sur une voiture miniature une échelle 1/64e,                      cela signifie que 1cm sur le modèle réduit correspond à 64cm dans la réalité.                      Sur un planisphère, l'échelle 1/750 000 000 signifie                      1cm pour 7500km (750 000 000cm = 7500km) Un tableau de proportionnalité permet de calculer certaines distances sur une carte.                ex: Soit une échelle 1/50 000 sur une carte.  Distance sur la carte (en cm) 1 7 ?  Distance réelle (en m) 500 ? 12 000    On trouve donc que 7cm sur la carte représentent:       7 x 500 = 3500m en distance réelle.    et que 12km (12 000m) en distance réelle représentent:       12 000 : 500 = 24cm sur la carte. IV. Pourcentage Un pourcentage est un coefficient de proportionnalité qui est noté en fraction et dont le dénominateur est 100.             30% se lit trente pour cent et est applicable en mathématiques par la fraction:              30              100 Pour calculer un pourcentage, on multiplie donc le nombre de départ par la fraction représentant le pourcentage:                ex: 30% de 120€.                                           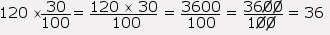donc 30% de 120€ représentent 36€. Le pourcentage étant un coefficient de proportionnalité, on peut utiliser un tableau pour en chercher une valeur: 30 36 ? 100 120 350    On trouve donc que 30% de 350 représentent:       350x30 : 100       = 10500 : 100       = 105 Enfin, pour déterminer un pourcentage, on doit ramener une fraction à une fraction sur 100.                ex: Une veste qui coûtait 140€ n'en coûte plus que 112€.                      Quel est le pourcentage de réduction?                      140€ représente les 100% du prix, et 112€ est le nouveau prix. 140 100 112 ?                      112x100 : 140                      = 11200 : 140                      = 80                      Le nouveau prix représente 80% de l'ancien prix,                      donc la réduction est de 100% - 80% = 20%. Des exercices d'application sur les proportions et les échelles sont disponibles  programme officiel     |     contactez un professeur     |     cours particuliers     |      haut de la page