Centre de Gravité et barycentre

I. Centre de gravité Son nom vient du phénomène de gravité, par lequel la Terre attire tous les objets pesants (= qui ont une masse) vers elle. D'une manière générale, le corps à la masse la plus élevée attire tous ceux à proximité dont la masse est plus faible. Le centre de gravité s'associe alors à la notion d'équilibre. Un corps, selon sa position, sera stabilisé, tombera ou se mettra en rotation.         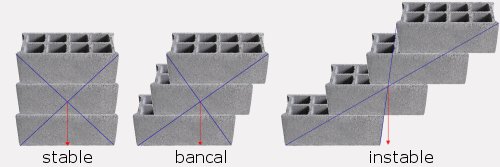1:. Objet posé Le centre de gravité peut-être assimilé au centre géométrique du corps, c'est-à-dire l'intersection des diagonales. On détermine la force de la gravité comme étant perpendiculaire au sol, donc verticale. Si la verticale passant par le centre de gravité passe aussi par la base de l'objet, celui-ci tient en équilibre. Sinon il tombe.         2:. Objet suspendu Un objet suspendu se positionne en équilibre quand il y a autant de matière (en masse) de part en d'autre (devant, derrière, à gauche, à droite) de la ligne de gravité, c'est-à-dire la verticale passant par le centre de gravité.                 ex1: Le fil à plomb est un objet est un objet de masse uniforme permettant de vérifier la verticalité.                 ex2: Si un objet plus lourd à droite qu'à gauche doit être suspendu,                        il ne faudra pas le faire par le milieu mais par un point décalé sur la droite                        pour répartir équitablement la masse. ! Le point d'intersection de deux lignes de gravité donne le centre de gravité, ce qui permet par exemple de déterminer le centre d'un cercle. II. Barycentre Pour étudier le centre de gravité d'un objet (ou système de plusieurs objets), on étudie le centre de gravité entre des points dotés de masses appelé barycentre. Il est la position moyenne de tous les points du système pondérée par la masse de chaque point. ! Le barycentre (étym.: centre des poids) est un point représentant la moyenne de plusieurs points pondérés (=qui ont une masse), alors que le centre de gravité d'un solide est son point d'équilibre, à la verticale du point de suspension.         1:. Barycentre de deux points de même masse Une balance Roberval est constituée de deux plateaux à égale distance du centre de la balance. Elle se met à l'équilibre lorsque la masse dans chaque plateau est identique. Le centre de poids, donc le barycentre, est au milieu de la balance. Les deux points sur la balance ayant la même masse, le centre de gravité est au milieu du segment délimité par ces deux points.         2:. Barycentre de deux points de masses différentes Si les masses des objets sur la balance sont différentes, il faut alors modifier les longueurs des bras portant les plateaux, pour compenser et rééquilibrer les masses et ainsi trouver le barycentre. ex: Si un objet a une masse deux fois plus importante que l'autre, le barycentre sera situé au 1/3 de la longueur du bras du côté de l'objet le plus lourd. 1/3 x 2m = 2/3 x 1m ! Si on rapproche du barycentre les deux masses de manière proportionnelle, l'équilibre est conservé jusqu'à concentrer la totalité de la masse au point G (barycentre). . Archimède (250 av. J.-C) affirme que "tout corps pesant a un centre de gravité bien défini en lequel tout le poids du corps peut être considéré comme concentré." . Huygens (1629-1695) énonce le principe d'équivalence du barycentre: "Le barycentre d'un système matériel se meut comme si toute la masse du système y était transportée, les forces extérieures du système agissant toutes sur ce barycentre." III. Application Le principe d'équivalence et la recherche de barycentre vont nous aider à trouver le point d'équilibre d'un objet complexe, à base de formes géométriques usuelles. 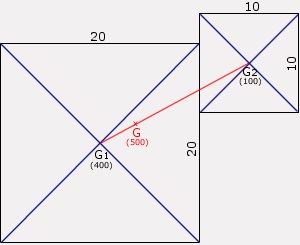Cet objet est formé de deux carrés. Le centre de gravité du carré est son centre géométrique, à l'intersection de ses diagonales. En appliquant le principe d'équivalence, il est possible de concentrer la masse de chaque carré en son centre:       G1 => 20 x 20 = 400       /      G2 => 10 x 10 = 100 Nous avons donc de deux points de masse différente. Si nous en calculons le barycentre, nous aurons le centre de gravité de cette forme particulière. Le point d'équilibre sera sous le carré le plus lourd, à une distance proportionnelle à la somme des deux masses cumulées (400+100 = 500), pour compenser l'écart de masse avec le carré le plus léger.  programme officiel     |     contactez un professeur     |     cours particuliers     |      haut de la page