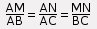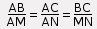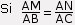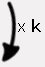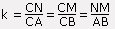Théorême de Thalès

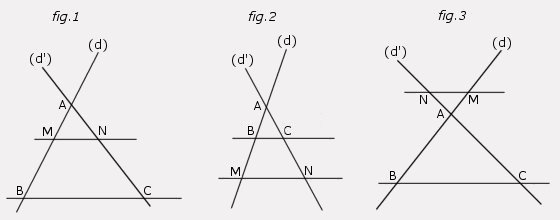
I. Idée générale Thalès est un savant grec ayant vécu au VIè siècle avant JC, à Milet, en Grèce. Le théorême de Thalès sert à connaître des longueurs dans un triangle en fonction d'autres longueurs. Il applique un rapport de longueurs qui peut se résumer dans un tableau de proportionnalité. On peut aussi l'utiliser pour démontrer que 2 droites sont parallèles. II. Le théorême Soit (d) et (d') deux droites sécantes en A. B et M sont 2 points de la droite (d), distincts de A. C et N sont 2 points de la droite (d'), distincts de A. 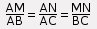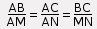Si les droites (BC) et (MN) sont parallèles alors: Grâce à la proportionnalité, on peut aussi écrire que:       Application: III. La réciproque du théorême Soit (d) et (d') deux droites sécantes en A. B et M sont 2 points de la droite (d), distincts de A. C et N sont 2 points de la droite (d'), distincts de A. 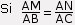et les points A,M,B sont alignés dans le même ordre que les points A,N,C alors les droites (MN) et (BC) sont parallèles.       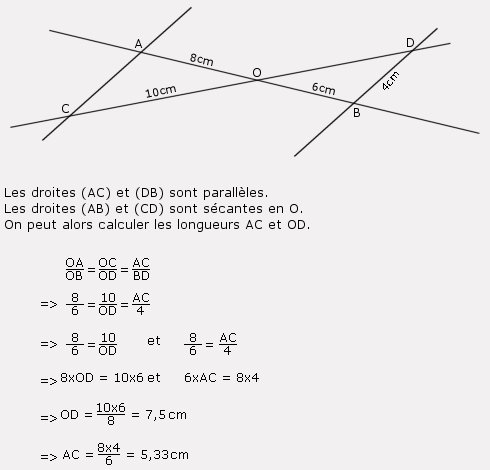Application: Les points A,M,B sont alignés dans le même ordre que les points A,N,C donc les droites (MN) et (BC) sont parallèles. IV. 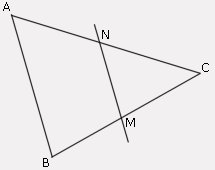Tableau de proportionnalité Soit un triangle ABC. La droite (MN) est parallèle à la droite (AB), donc le théorême de Thalès s'applique. On obtient alors que les longueurs des côtés du triangle NMC sont proportionnelles aux longueurs des côtés correspondants du triangle ABC, et on peut remplir le tableau de proportionnalité. 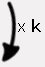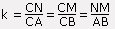côtés de NMC CN CM NM côtés de ABC CA CB AB k est le coefficient de proportionnalité tel que: Des exercices d'application du théorême de Thalès sont disponibles  programme officiel     |     contactez un professeur     |     cours particuliers     |      haut de la page