Le Parallélogramme - ses propriétés

I. Idées générales Un parallélogramme est une figure géométrique à 4 côtés, un quadrilatère. Les propriétés du parallélogramme vont permettre de démontrer qu'une figure est un parallélogramme.        ex: Etant donné que cette figure à (...), alors on peut dire qu'elle est un parallélogramme. Inversement, la réciproque se base sur le fait qu'on sache déjà que la figure est un parallélogramme, donc on peut en déduire autre chose.              ex: On sait que cette figure est un parallélogramme, donc on sait automatiquement que (...). II. 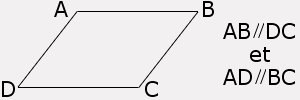Propriétés P1: Un quadrilatère qui a ses côtés opposés 2 à 2 parallèles est un parallélogramme. 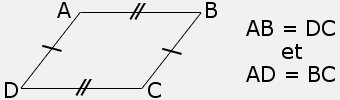P2: Un parallélogramme a ses côtés opposés 2 à 2 de même longueur. P3: Un parallélogramme a ses angles opposés 2 à 2 de même mesure. 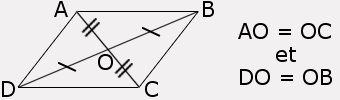P4: Un parallélogramme a ses diagonales qui se coupent en leur milieu. P5: Un parallélogramme a pour centre de symétrie l'intersection de ses diagonales. Ces 5 affirmations sont valables pour tous les parallélogrammes. Ainsi, quand on obtient un de ces cas de figure, on sait que le quadrilatère sera un parallélogramme. On peut alors énoncer les propriétés démontrant qu'un quadrilatère est un parallélogramme: 1. Si un quadrilatère a ses côtés opposés 2 à 2 de même mesure alors c'est un parallélogramme. 2. Si un quadrilatère a ses angles opposés 2 à 2 de même mesure alors c'est un parallélogramme 3. Si un quadrilatère a ses diagonales qui se coupent en leur milieu alors c'est un parallélogramme. 4. si un quadrilatère a un centre de symétrie alors c'est un parallélogramme. 5. Si un quadrilatère à deux côtés parallèles et de même longueur alors c'est un parallélogramme. 6. Si un trapèze à ses côtés parallèles de même longueur alors c'est un parallélogramme. Carte mentale imprimable  programme officiel     |     contactez un professeur     |     cours particuliers     |      haut de la page